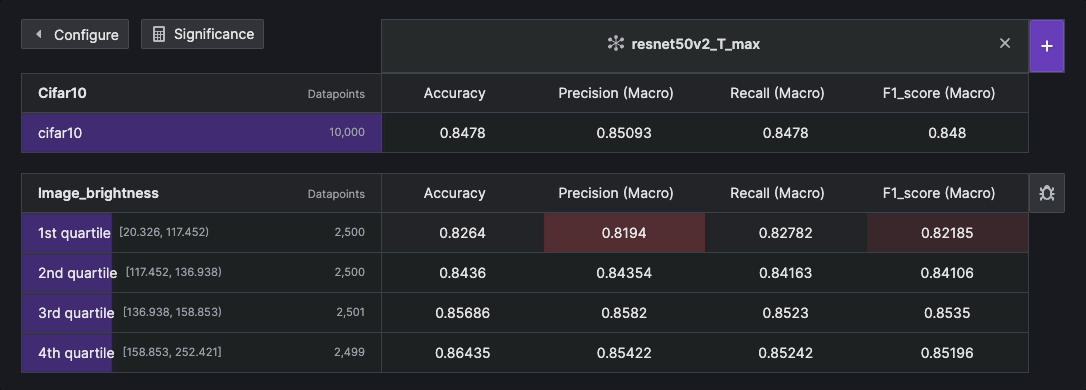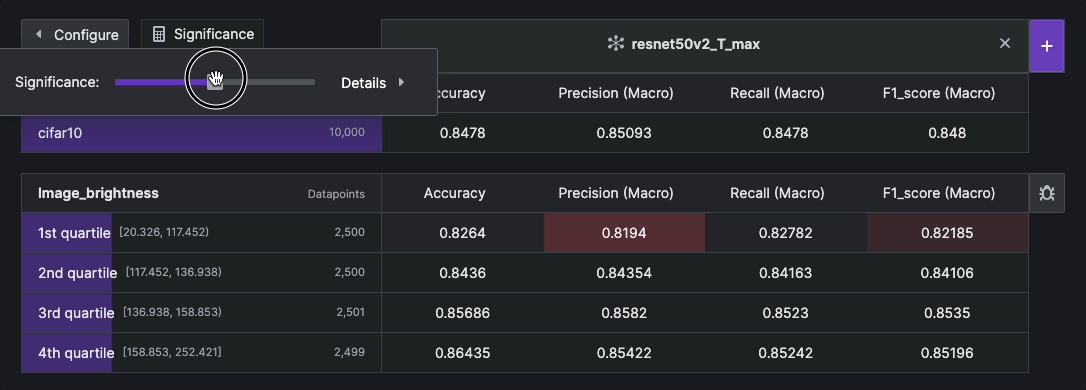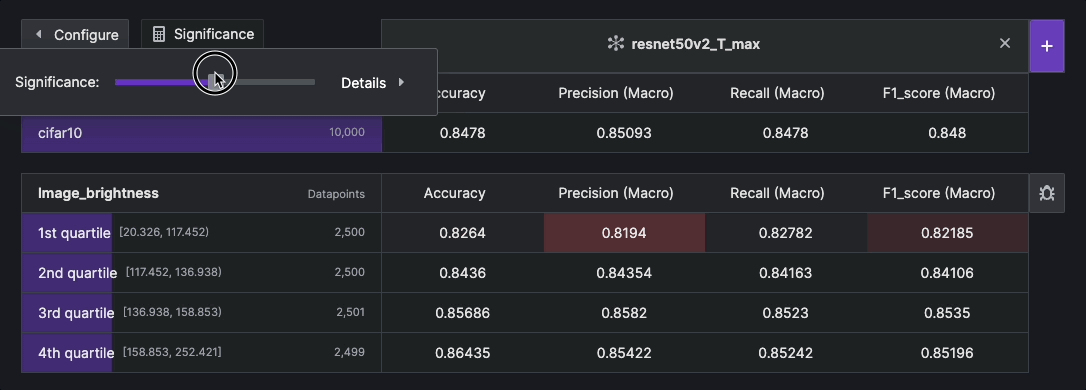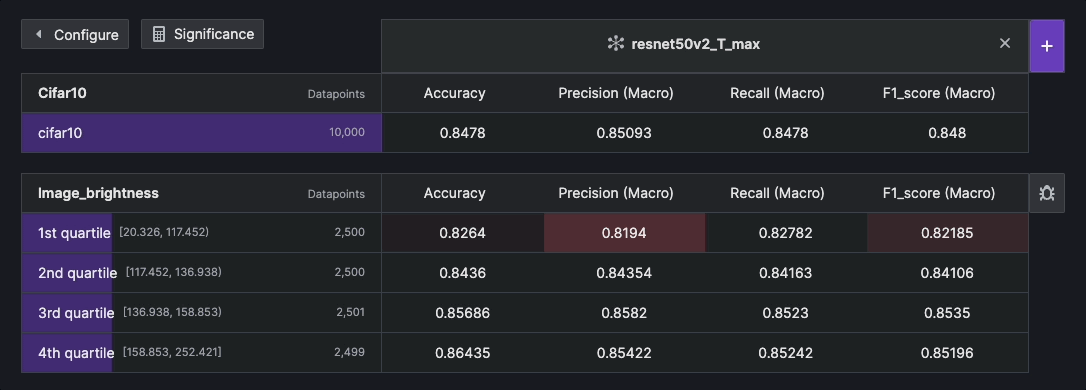
Statistical Significance#
Statistical significance refers to the degree of certainty that observed differences in a result are not due to random chance. It is often used by researchers to draw meaningful conclusions and make informed decisions based on their analysis. Within the context of Kolena, it is used as a statistical representation of the amount of tolerance in the evaluation results based on the chosen confidence level and the size of a test case. This significance is calculated by estimating the margin of error (MOE), which ranges from 0% to 100%. The larger the MOE, the less confidence one should have that a result would reflect the complete representation of the test case.

Implementation Details#
To calculate the statistical significance, it is necessary to compare the calculated MOE with the observed difference. If the observed difference is larger than the MOE, it suggests that the difference is statistically significant at the chosen confidence level. Conversely, if the observed difference is within the MOE, it indicates that the difference is not statistically significant.
Margin of Error (MOE)#
The MOE is determined by two factors: the sample size and the desired level of confidence. Larger sample sizes yield smaller MOE, as they provide more reliable estimates of the population. The level of confidence represents the probability of capturing the true population parameter within the calculated MOE.
Generally, at a confidence level \(\gamma\), a sample sized \(n\) of a population having an expected proportion \(p\) has a MOE:
where
- \(z_{\gamma}\) is the z-score
- \(\sqrt{\frac{p(1 - p)}{n}}\) is the standard error
Confidence Level (\(\gamma\))
Commonly used confidence levels are 0.90, 0.95, and 0.99.
| Confidence Level (\(\gamma\)) | z-score |
|---|---|
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Standard Error
The standard error is often unknown. The common practice is using an approximation value. Consequently, if there is no information available to approximate it, then \(p = 0.5\) can be used to generate the most conservative significance score.
Examples#
Imagine you have an AI model that has been tested with 1,000 randomly selected datapoints from your test set that represent the data from your deployment site.
The results from the test indicate that of these 1,000 datapoints, 52% (520 datapoints) were predicted correctly, while 48% (480 datapoints) were not. What is the margin of error of your test results at the 95% confidence level?
To use the formula above, we need to first calculate all the variables.
The \(z_{0.95}\) is 1.96. The \(p\) value is the positive sample rate, so it's simply \(\frac{520}{1,000} = 0.52\). The \(n\) is the sample size which is \(1,000\).
Plugging these values into the formula, we get:
You can report with 95% confidence that your model achieved 52% accuracy, with a margin of error of \(\pm\) 3.1%.
Let's say we have another model tested on the same 1,000 datapoints, and it's accuracy is 54%, which is 2% higher than the first model's accuracy. Given the calculated MOE, the difference in accuracy is not statistically significant because it falls within the MOE.
Finally, we have a third model tested on the same 1,000 datapoints, but this time its accuracy is 80%, which is 28% more than the first model's accuracy. Given the calculated MOE, this difference in accuracy is statistically significant; therefore, we can be 95% confident that the third model performs better than the first model.
If you ever wonder whether a small observed difference in your model results is statistically significant, you can reduce the margin of error by increasing the sample size of your test. When we take a larger sample size, we increase the representation of the population in the sample, which reduces the margin of error.
Limitations and Biases#
The margin of error is a good metric that can be used to understand the statistical significance of your model results; however, there are some limitations that we need to be aware of.
-
The MOE calculation assumes a normal distribution on a sufficiently large sample size.
-
The exact MOE calculation requires the sample proportion or population standard deviation, which is often unknown.
-
There are many factors beyond sample size and data variability that determine practical significance in the real life. Statiscially significant results can be obtained even with a negligible effect if the sample size is large and the variability is low. In such situations, though the effect likely exists, its real-world impact is typically minimal.
Keep these limitations in mind when you are using statistical significance in your application. It is a great guideline that can help you highlight what you need to pay attention to when analyzing your test results.